Published on

BlueHensCTF 2023 - Appetizers

Authors

Appetizers

A deep dive into a cryptographic puzzle influenced by the NP-Complete Subset Sum Problem.

Table of Contents

Introduction

The Appetizers challenge presented participants with a cryptographic puzzle deeply intertwined with the Subset Sum Problem, a renowned problem in computational theory.

The Humor and Complexity Behind the XKCD Image

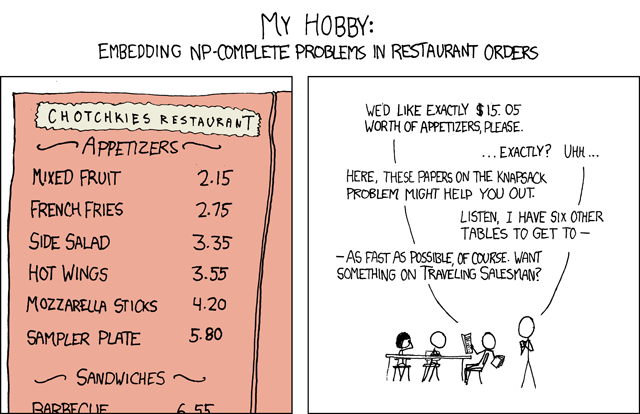
NP-Complete Problem

The XKCD comic subtly conveys the intrigue surrounding NP-Complete problems. At a glance, the image humorously juxtaposes the idea of a simple task, like finding a university department, with the complexity of an NP problem, suggesting that even mundane tasks can be formulated as intricate computational problems. This comedic exaggeration underscores the pervasive nature of NP-Complete problems, indicating that they can be found even in seemingly simple challenges. In essence, the comic cleverly communicates the idea that, in the world of computer science, even straightforward tasks can have underlying complexities that make them as challenging as renowned problems.

Understanding the NP-Complete Subset Sum Problem

The Subset Sum Problem revolves around identifying if there's a subset within a given set of numbers that, when summed up, equals a predetermined target number. Its classification as NP-Complete means that while verifying a solution is feasible in polynomial time, finding one might not be.

Challenge Script Analysis 

#Subset Sum Problem
#https://imgs.xkcd.com/comics/np_complete.png
import random
choices = list(set([random.randint(100000,1000000000) for _ in range(30)]))
random.shuffle(choices)
winners = choices[:15]
target = sum(winners)
winners.sort()
flag = "UDCTF{%s}" % ("_".join(map(str,winners)))
#print(flag)
choices.sort()
print(choices)
print(target)

'''
Output:

[19728964, 30673077, 137289540, 195938621, 207242611, 237735979, 298141799, 302597011, 387047012, 405520686, 424852916, 461998372, 463977415, 528505766, 557896298, 603269308, 613528675, 621228168, 654758801, 670668388, 741571487, 753993381, 763314787, 770263388, 806543382, 864409584, 875042623, 875651556, 918697500, 946831967]
7627676296
'''

This script generates a set of 30 unique random numbers. From this, a subset of 15 numbers is chosen. Their cumulative sum becomes the target value, and the flag is constructed from this subset.

Solution to the Challenge

Using Python's itertools library, the solution employs a brute-force approach, iterating through number combinations to identify the subset equating to the target sum.

import itertools

choices = [19728964, 30673077, 137289540, 195938621, 207242611, 237735979, 298141799, 302597011, 387047012, 405520686, 424852916, 461998372, 463977415, 528505766, 557896298, 603269308, 613528675, 621228168, 654758801, 670668388, 741571487, 753993381, 763314787, 770263388, 806543382, 864409584, 875042623, 875651556, 918697500, 946831967]
target = 7627676296

def find_subset_sum(numbers, target_sum):
    for r in range(1, len(numbers) + 1):
        for subset in itertools.combinations(numbers, r):
            if sum(subset) == target_sum:
                return subset
    return None

subset = find_subset_sum(choices, target)
if subset:
    subset = sorted(list(subset))
    flag = "UDCTF{%s}" % ("_".join(map(str,subset)))
    print(flag)
else:
    print("No subset found.")

On executing this solution script, the flag is revealed.

Flag : UDCTF{19728964_30673077_137289540_195938621_237735979_302597011_463977415_603269308_654758801_670668388_763314787_806543382_875651556_918697500_946831967}

Conclusion

The Appetizers challenge was a compelling fusion of computational theory, cryptography, and humor. It highlighted the intricacies of NP-Complete problems and the importance of understanding the foundations of computational challenges, reminding us that beneath seemingly simple problems can lie profound complexities.